Linear Regression

-

What is Regression?

A measure of the relation between the continuous dependent variable(e.g. output) with one/many discrete/continuous independent variables(e.g. input).
In Machine Learning, Regression is a supervised statistical predictive model.
Other statistical models are Descriptive model , Prescriptive model etc.

Different Types of Regression model in Machine Learning

In Machine learning, There are mainly  Three types  of  Regression model.

  • Linear Regression Model 

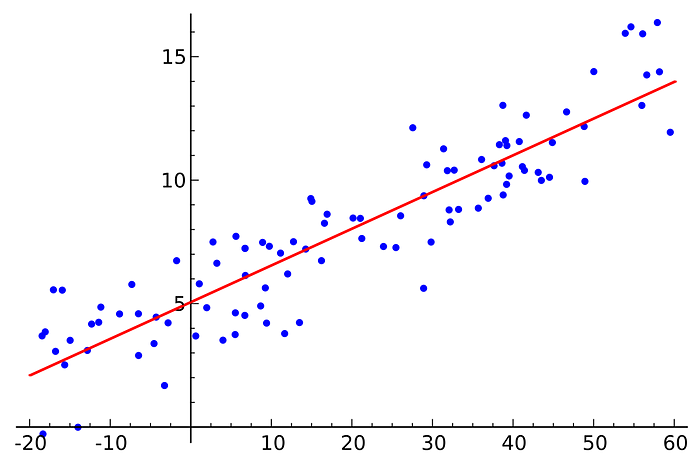
In this type of predictive model, The relationship between the Independent and Dependent Variables can be  represented as straight line(single/multiple particularly where clusters are present).
linear regression

  • Polynomial Regression Model
In this type of predictive model, The relationship between the Independent and Dependent Variables can be  represented as polynomial curve(single/multiple particularly where clusters are present).
Polynomial Regression Model

  • Logistic Regression Model
 It is special type of classification model where this model can classify dependent variable in different classes(Binomial for 2 classes/Multinomial for more than 2 classes) where it use a linear model implicitly.

Logistic Regression Model

In this post we are going to see about the most simple REGRESSION MODEL (LINEAR) 


To listen this page please open the player

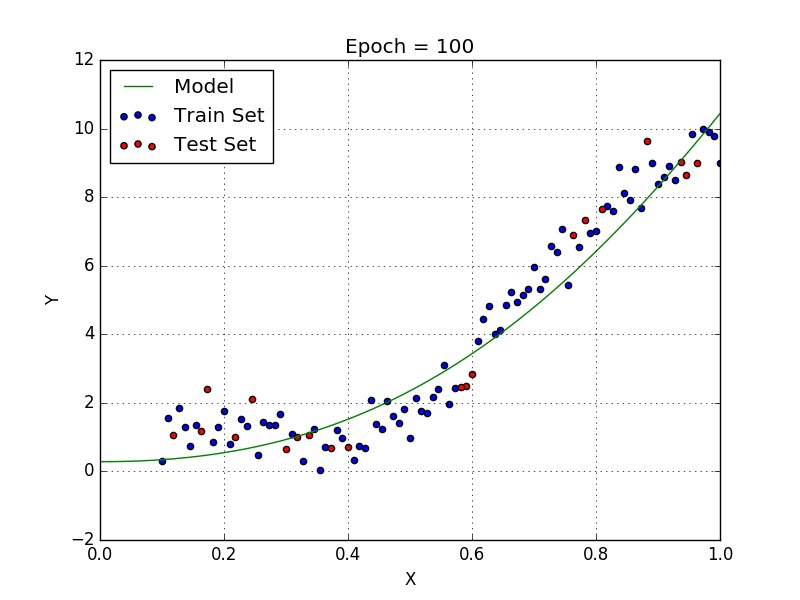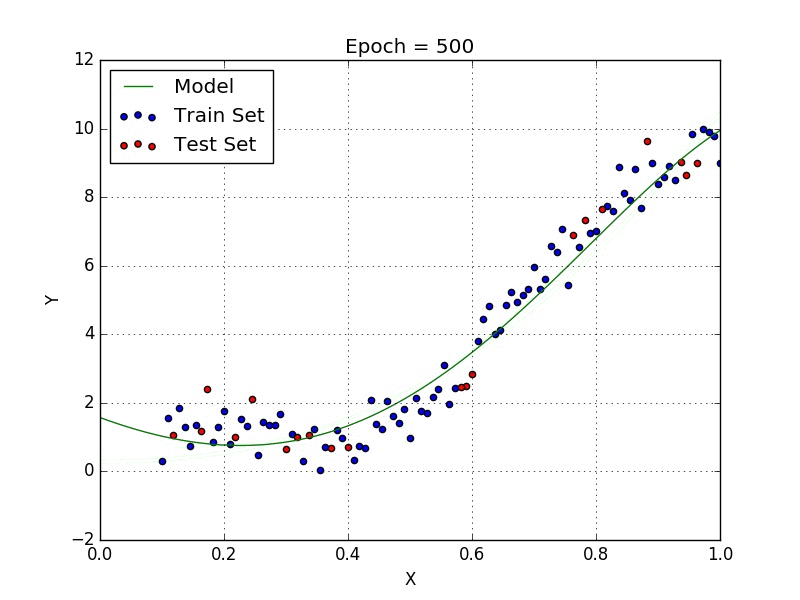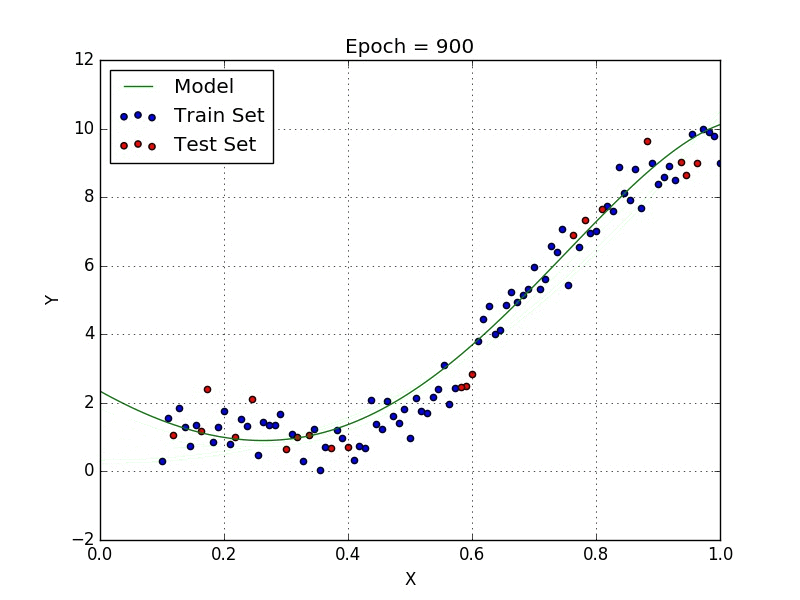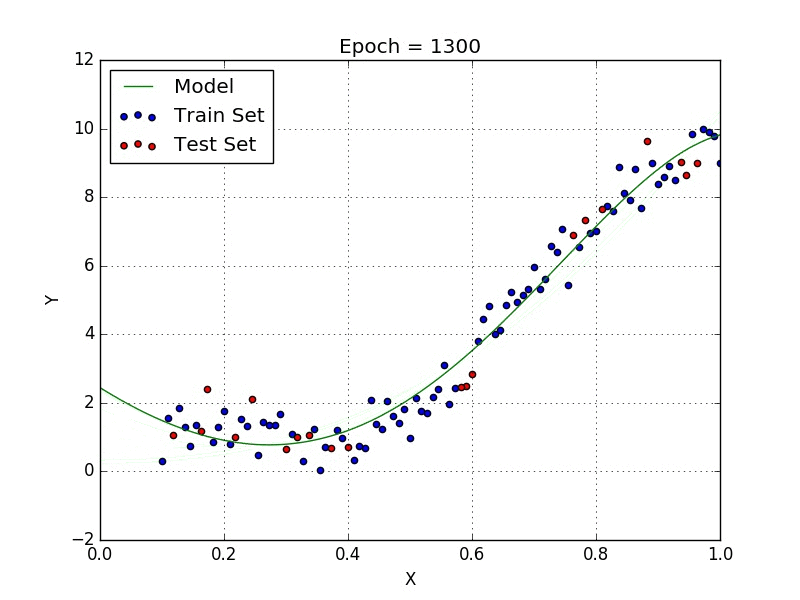
Basics of Linear Model in Machine Learning:

Here, using linear model we express the dependent variable(Y) in terms of independent variables(X1, X2, X3)  
    Y = b0 + b1*x1+b2*x2+b3*x3
Here, we have taken 3 independent variables only.
We choose the best fit straight line by minimizing the mean of sum of squared error(MSE).
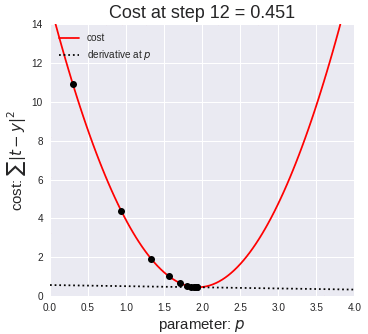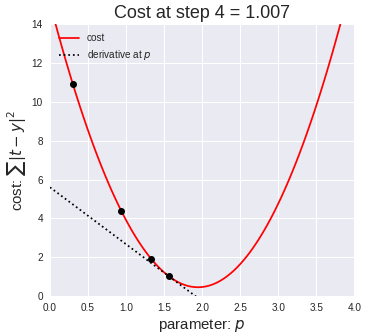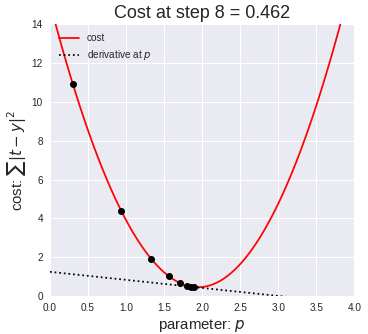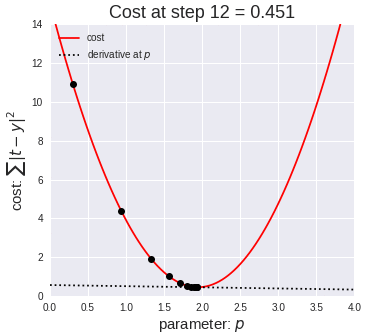
From that if we minimize the summation of squared error then also we can able to minimize the above expression. This function is called Cost function.

error
From the cost function we can get the coefficients(or weights) of each independent variable by equating the first derivative of the cost function equals to Zero.

cost function


NOTE: 
If we have bivariate data, then from the above expression we will get a very beautiful result.
 Y = b0 + b1*x    [ For Bivariate Data ]
Then we will get these result, given as -
                 b1 = cov(x,y)/var(x)
                 b0 = E(y)-b1*E(x)
where E(x) and E(y) gives the mean of x and y respectively.

Reasons for using MSE(mean squared error) over MAE(mean absolute error)

  • Cost function, as being quadratic function, is a continuous differentiable function. That's why we get a global minima that ensures the best fit line.
  • On the other hand, |x| function is continuous but a non differentiable function we can not do the previous steps.

Disadvantage of using MSE(mean squared error)

  • If the Error is very large then the square of it will become a very large number. Then for our simplicity we will use different types of error estimation function

Conclusion:

From the above concept we have learnt about What Regression problem is and What is linear regression. For the next concepts please go though the other posts of Data Science.


Comments

Post a Comment

Popular posts from this blog

Introduction to Computer Vision

-
Image
  Do you ever think, how Facebook can automatically tag your friend when you upload an image, how your smart phone can recognize you, using it's very advanced and accurate  Face recognition feature.  Have you ever thought how a picture is processed by computer , how a picture  is stored in computer  etc.   These are very few examples, many more will be discussed as we go on, of Computer Vision. Well, In this post we are going to discuss about Computer Vision. So let's get started. What is C omputer Vision ? Computer Vision is a  interdisciplinary field that helps computer to make high-level understanding from digital images and videos to automate the task that human visuals do. It use some techniques  by which computer can understand many useful information from an image and perform some action based on that information. We see an image and our brain can understand the message, delivered by the image. Machines do exactly the same thing. ...
Read more

Distance measurement using opencv

-
Image
In Covid-19 pandemic, we all know about the importance of Social Distancing . Right now, It is the only thing that can help to reduce the number of affected people. So I have decided to make a social distancing checker using python. The main idea is to measure the distance of object in the image and if the distance between two objects are less than some predefined pixel value then 'green' dot at the center of the bounding-box will convert to 'red' dot . The output of the code will like this- social distancing checker Python code for Distance Measurement I am providing the python code to measure the distance of the object in the image or each frame of a video. Later I will discuss some key points related to the code. Key points to be Noted: Everything will be the same like object detection (discussed in Part-I and Part-II ) as I have implemented distance measurement based on object detection. We will filter out only the  'person' object   from the obje...
Read more

Object Detection (PART-II)

-
Image
  The  most fundamental computer technology  related to Computer vision and Image Processing is  Object Detection.  It deals with detecting the   semantic object of a certain class in digital images and videos. In the previous post, I have shown you how to detect object very easily with less than 15 lines of code. But our concern is about the FPS(Frames Per Second). Check out the  Object Detection (PART-I)    if you have not seen yet.  In this post, we are going to optimize the previous post so that we can improve the FPS. In this case also we are gong to use YOLO  model again. There are 80 different classes that can be detected using YOLO model. such as-       person, bicycle, car, motorcycle, airplane, bus, train, truck, boat, traffic light, fire hydrant, stop_sign, parking meter, bench, bird, cat, dog, horse, sheep, cow, elephant, bear, zebra, giraffe, b...
Read more